Parametric Equalizer x16 Stereo
Detailed: LSP Parametric Equalizer x16 Stereo (PE16S)
Formats: CLAP, JACK, LADSPA, LV2, VST2, VST3
Categories: Parametric Equalizer
Developer: Vladimir Sadovnikov
Description:
Digital filters can be classified into two big categories - Finite Impulse Response (FIR) filters and Infinite Impulse Response (IIR) filters.
Finite impulse response filters have limited impulse characteristic (the filter's reaction on the single pulse) in time domain. That causes that filters have weak resolution in frequency domain when the length of impulse response is short and have very good resolution in frequency domain when the length of impulse response is large. With large impulse response FIR filters can be times better than IIR filters but the main disadvantage of FIR filters is the necessity to do many calculations to perform convolution of input signal with impulse response of the filter. Thanks Fast Fourier Transform (FFT) algorithms the convolution may be calculated times faster rather than using direct convolution algorithm.
Infinite impulse response filters work as systems that process input signal and some part of already processed signal (feedback). Thanks such behaviour they have infinite impulse response in time domain. The final equation of these filters is times smaller than for similar by characteristics FIR filters, so they need less CPU time for processing. The disadvantage of IIR filters is that they are limited in form of their spectral characteristics. Also, IIR filters are mostly the digital representation of analog filters.
FIR filters can be zero-phase (only when performing offline processing), linear-phase and non-linear phase (when performing offline and realtime processing). IIR filters never can have linear phase characteristic while performing realtime processing, only in offline mode. The difference of linear-phase and non-linear phase of filters is that when summarizing the same signal processed by linear-phase filter, we become no phase distortion that can cause unwanted frequency peaks or pits in some frequency range. With IIR filters frequency distortion is often practice rather than exception. The disadvantage of FIR filters is that due to long impulse response of the linear-phase FIR filter (that is symmetric in time line with peak at center) we get noticeably delayed signal after filtering stage.
LSP Plugins provide three types of filters - already known IIR and two types of FIR filters - FIR and FFT. The difference between FIR and FFT filter modes is how these filters are built. FIR filters are built from impulse response of similar IIR filter, and then transformed so that they become linear phase characteristic. FFT filters are build by using frequency characteristic of FIR filter. Finally, both use FFT convolution to perform fast signal processing.
All filters are build by using well-known methods of analog filter design (complex polynomials in top and bottom) or directly as digital filters. When the filters are build from analog designs, plugins first of all calculate parameters of ideal analog filter by using Laplace transform and then digitize it by applying analog-to-digital transform also known as Z Transform. Each filter implements it's own set of poles and zeros, the configuration of poles and zeros can be controlled by using quality factor and slope parameters.
There are set of rules to perform Laplace to Z-space transformation, for example Simpson rule etc. In LSP plugins, two types of rules are used: the most popular Bilinear Transform and less popular Matched Z Transform. The difference between these transforms is how the frequency and ampitude characteristics are moved from analog form into digital.
Bilinear Transform is easy to implement, and in most plugins this type of transform is used. The main disadvantage of this transform is that it distorts the form of the filter's curve while moving it's poles and zeros from low to high frequencies. Also it's noticeable that low-pass filters transformed by using bilinear transform have -INF dB amplification level at the Nyquist frequency.
Completely different is the behaviour of filters transformed by Matched Z Transform. These filters have identical to the analog filters frequency and phase graph but have another disadvantage: they have aliasing at high frequencies that is caused by reflecting high frequencies from the range limited by Nyquist Frequency.
Digital filters can also be generated directly in the digital domain, without needing to convert an analog prototype or by using design equations available in literature, often coming from digitalization of canonic analog filter prototypes, but with the advantage of not having to perform digitalization in real-time. This is the case of Direct design IIR filters.
Additional attention should be given to FIR filters because Bilinear Transform and Matched Z Transform advantages and disadvantages are only applicable to the IIR filters. FIR filters are free of this and just copy characteristics of IIR filters.
All filters are mostly of all frequently used filter types that can be required in studio production. There are available simple ideal RLC-filters (Resistor, Inductivity and Capacitor) that have very smooth frequency characteristics, Butterworth-Chebyshev-filters based on Butterworth-Chebyshev polynomials (BWC) and Linkwitz-Riley-based filters (LRX). So, shortly, RLC filters can be used for accurate frequency correction, BWC-based filters can be used for strong frequency correction and LRX-filters for extreme frequency correction.
All filters are designed to have clean sound and keep minimal phase shift if it's possible. They do not affect dynamics of the signal or colorize the original sound, they just perform correction in frequency domain. BT (Bilinear Transform) filters will have no distortion at high frequencies but will have distorted (relative to the similar analog filter) amplitude and frequency chart. MT (Matched Z Tranfrorm) filters can distort the signal at high frequencies because high frequencies can get reflected from Nyquist Frequency and that may cause aliasing effect. In fact, It's not audible in most cases.
There are some recommendations that could be given when applying equalization:
- Resonance filter with high Quality Factor can be good choice to cut annoying masking resonances from the original sound.
- Bell filter with medium Quality Factor can be used when there is necessity to remove short range of frequencies.
- Bell filter with low Quality Factor can be used to raise or lower wide range of frequencies.
- Shelving filters with low Quality Factor also can be used to lower or raise the large diapasone of frequencies.
- Low-pass and High-pass filters can be used with a bit raised Quality Factor to flatten frequency fall. Usage of Butterworth-Chebyshev low-pass and high-pass filters with 2x and 3x slope can give good results when cutting unwanterd low and high frequencies from voice or guitar sound.
- Matched Z Transform (MT) filters are probably the best choice when cutting out individual short range of frequencies.
- Bilinear Transform (BT) filters are good when cutting-out high frequencies because they have -INF dB amplification at the Nyquist frequency.
- Direct Design (DR) filters add alternative implementations for the various supperted filter types, and may be chosen whenever their frequency response is best suited.
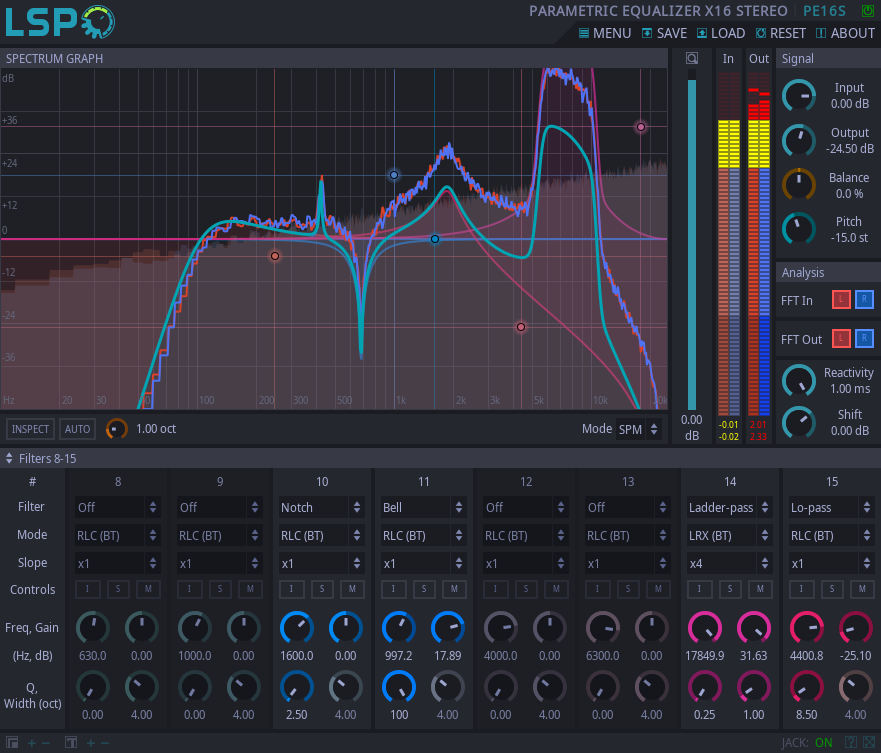
This plugin performs parametric equalization of stereo channel. Up to 16 filters are available for signal processing simultaneously.
Additional filter inspection feature with the controlled width of the bandpass filter allows to listen the frequency band around several filter types to make search and cut off resonances much easier:
The steepness of the filter is depending on the type of the filter selected, it's slope and Q factor.
There is a simple rule that allows to compute the steepness of IIR (recursive) low-pass or high-pass filter which consists of so-called poles and zeros:
- each pole gives -6 dB/octave magnitude attenuation above the pole's frequency;
- each zero gives +6 dB/octave magnitude amplification above the zero's frequency.
That allows to make the following conclusions:
- the more poles are used by the filter, the more steep magnitude attenuation will be;
- when talking about the magnitude, each zero cancels the pole's attenuation curve and vice verse, depending on their locations in the frequency domain;
- the filter can not contain more zeros than the number of poles. Otherwise it will give infinite magnitude at the infinite frequency;
- the slope of simple filers is a discrete value with step of -6 dB/octave.
There is a table that specifies characteristics of lowpass filters depending on the selected filter mode and slope.
| Mode | Poles | Slope (dB/oct) | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x1 | x2 | x3 | x4 | |
| RLC | 2 | 4 | 6 | 8 | -12 | -24 | -36 | -48 |
| BWC | 2 | 4 | 6 | 8 | -12 | -24 | -36 | -48 |
| LRX | 4 | 8 | 12 | 16 | -24 | -48 | -72 | -96 |
| APO | 2 | 2 | 2 | 2 | -12 | -12 | -12 | -12 |
Adjusting q can give additional steepness to the curve but making it too high gives extra non-linearity of the magnitude in the passed spectrum.
- Bell-shaped filters;
- Notch filters;
- Resonance filters;
- Hi-shelving filters;
- Lo-shelving filters.
The frequency control feature allows to detect the note and the note detune the filter is operating with at the top of the graph area.
Additionally, mouse double-click on the graph area allows to add a filter with desired frequency and gain settings depending on the actual frequency value at the position of the mouse click:
- 20 Hz and below: Hi-pass RLC BT filter with Q=0.5;
- 20 Hz - 50 Hz: Lo-shelf RLC BT filter with Q=0.5;
- 50 Hz - 5 kHz: Bell RLC BT filter with Q=2;
- 5 kHz - 15 kHz: Hi-shelf RLC BT filter with Q=0.5;
- 15 kHz and above: Lo-pass RLC BT filter with Q=0.5.
Several filter parameters like type, mode, slope, inspection, solo and mute are also available for change from the context menu which can be displayed by the right mouse click over the filter's control dot in the graph area.
Meters:
- Input - the level meter for left and right channels of the input signal.
- Output - the level meter for left and right channels of the output signal.
Controls:
- Bypass - bypass switch, when turned on (led indicator is shining), the plugin bypasses signal.
- Mode - equalizer working mode, enables the following mode for all filters:
- IIR - Infinite Impulse Response filters, nonlinear minimal phase. In most cases does not add noticeable latency to output signal.
- FIR - Finite Impulse Response filters with linear phase, finite approximation of equalizer's impulse response. Adds noticeable latency to output signal.
- FFT - Fast Fourier Transform approximation of the frequency chart, linear phase. Adds noticeable latency to output signal.
- SPM - Spectral Processor Mode of equalizer, equalizer transforms the magnitude of signal spectrum instead of applying impulse response to the signal.
- Left - enables the FFT analysis for the left channel.
- Right - enables the FFT analysis for the right channel.
- Zoom - zoom fader, allows to adjust zoom on the frequency chart.
- Inspect - the button that disables the inspect mode for currently selected filter.
- Auto - the button that enables automatic filter inspection for the currently edited filter.
- Inspect knob - the knob that controls the bandwidth of the bandpass filter around the inspected filter.
'Signal' section:
- Input - input signal amplification.
- Output - output signal amplification.
- Balance - balance between left and right output channels.
- Pitch - the frequency shift for all filters, in semitones.
'Analysis' section:
- FFT - enables FFT analysis before or after processing.
- Reactivity - the reactivity (smoothness) of the spectral analysis.
- Shift - allows to adjust the overall gain of the analysis.
'Filters' section:
- Filter - sets up the mode of the selected filter. Currently available filters:
- Off - Filter is not working (turned off).
- Bell - Bell filter with smooth peak/recess.
- Hi-pass - High-pass filter with rejection of low frequencies.
- Hi-shelf - Shelving filter with adjustment of high frequency range.
- Lo-pass - Low-pass filter with rejection of high frequencies.
- Lo-shelf - Shelving filter with adjustment of low frequencies.
- Notch - Notch filter with full rejection of selected frequency.
- Resonance - Resonance filter with sharp peak/recess.
- Allpass - All-pass filter which only affects the phase of the audio signal at the specified frequency.
- Mode - sets up the class of the filter:
- RLC - Very smooth filters based on similar cascades of RLC contours.
- BWC - Butterworth-Chebyshev-type-1 based filters. Does not affect Resonance and Notch filters.
- LRX - Linkwitz-Riley based filters. Does not affect Resonance and Notch filters.
- APO - Digital biquad filters derived from canonic analog biquad prototypes digitalized through Bilinear transform. These are textbook filters which are implemented as in the EqualizerAPO software.
- BT - Bilinear Z-transform is used for pole/zero mapping.
- MT - Matched Z-transform is used for pole/zero mapping.
- DR - Direct design is used to serve the digital filter coefficients directly in the digital domain, without performing transforms.
- Slope - the slope of the filter characteristics.
- I - the inspection button, allows to inspect selected filter.
- S - the soloing button, allows to solo selected filters.
- M - the mute button, allows to mute selected filters.
- Freq - the cutoff/resonance frequency of the filter.
- Gain - the gain of the filter, disabled for lo-pass/hi-pass/notch filters.
- Q - the quality factor of the filter.
- Hue - the color of the frequency chart of the filter on the graph.































