Parametric Equalizer x32 LeftRight

Parametrischer Entzerrer x32 LeftRight

Detailed: LSP Parametric Equalizer x32 LeftRight (PE32LR)

Formats: CLAP, JACK, LADSPA, LV2, VST2, VST3

Categories: Parametric Equalizer

Developer: Vladimir Sadovnikov

Description: 

Digital filters can be classified into two big categories - Finite Impulse Response (FIR) filters and Infinite Impulse Response (IIR) filters.

Finite impulse response filters have limited impulse characteristic (the filter's reaction on the single pulse) in time domain. That causes that filters have weak resolution in frequency domain when the length of impulse response is short and have very good resolution in frequency domain when the length of impulse response is large. With large impulse response FIR filters can be times better than IIR filters but the main disadvantage of FIR filters is the necessity to do many calculations to perform convolution of input signal with impulse response of the filter. Thanks Fast Fourier Transform (FFT) algorithms the convolution may be calculated times faster rather than using direct convolution algorithm.

Infinite impulse response filters work as systems that process input signal and some part of already processed signal (feedback). Thanks such behaviour they have infinite impulse response in time domain. The final equation of these filters is times smaller than for similar by characteristics FIR filters, so they need less CPU time for processing. The disadvantage of IIR filters is that they are limited in form of their spectral characteristics. Also, IIR filters are mostly the digital representation of analog filters.

FIR filters can be zero-phase (only when performing offline processing), linear-phase and non-linear phase (when performing offline and realtime processing). IIR filters never can have linear phase characteristic while performing realtime processing, only in offline mode. The difference of linear-phase and non-linear phase of filters is that when summarizing the same signal processed by linear-phase filter, we become no phase distortion that can cause unwanted frequency peaks or pits in some frequency range. With IIR filters frequency distortion is often practice rather than exception. The disadvantage of FIR filters is that due to long impulse response of the linear-phase FIR filter (that is symmetric in time line with peak at center) we get noticeably delayed signal after filtering stage.

LSP Plugins provide three types of filters - already known IIR and two types of FIR filters - FIR and FFT. The difference between FIR and FFT filter modes is how these filters are built. FIR filters are built from impulse response of similar IIR filter, and then transformed so that they become linear phase characteristic. FFT filters are build by using frequency characteristic of FIR filter. Finally, both use FFT convolution to perform fast signal processing.

All filters are build by using well-known methods of analog filter design (complex polynomials in top and bottom) or directly as digital filters. When the filters are build from analog designs, plugins first of all calculate parameters of ideal analog filter by using Laplace transform and then digitalize it by applying analog-to-digital transform also known as Z Transform. Each filter implements it's own set of poles and zeros, the configuration of poles and zeros can be controlled by using quality factor and slope parameters.

There are set of rules to perform Laplace to Z-space transformation, for example Simpson rule etc. In LSP plugins, two types of rules are used: the most popular Bilinear Transform and less popular Matched Z Transform. The difference between these transforms is how the frequency and ampitude characteristics are moved from analog form into digital.

Bilinear Transform is easy to implement, and in most plugins this type of transform is used. The main disadvantage of this transform is that it distorts the form of the filter's curve while moving it's poles and zeros from low to high frequencies. Also it's noticeable that low-pass filters transformed by using bilinear transform have -INF dB amplification level at the Nyquist frequency.

Completely different is the behaviour of filters transformed by Matched Z Transform. These filters have identical to the analog filters frequency and phase graph but have another disadvantage: they have aliasing at high frequencies that is caused by reflecting high frequencies from the range limited by Nyquist Frequency.

Digital filters can also be generated directly in the digital domain, without needing to convert an analog prototype or by using design equations availble in literature, often coming from digitalization of canonic analog filter prototypes, but with the advantage of not having to perform digitalization in real-time. This is the case of Direct design IIR filters.

Additional attention should be given to FIR filters because Bilinear Transform and Matched Z Transform advantages and disadvantages are only applicable to the IIR filters. FIR filters are free of this and just copy characteristics of IIR filters.

All filters are mostly of all frequently used filter types that can be required in studio production. There are available simple ideal RLC-filters (Resistor, Inductivity and Capacitor) that have very smooth frequency characteristics, Butterworth-Chebyshev-filters based on Butterworth-Chebyshev polynomials (BWC) and Linkwitz-Riley-based filters (LRX). So, shortly, RLC filters can be used for accurate frequency correction, BWC-based filters can be used for strong frequency correction and LRX-filters for extreme frequency correction.

All filters are designed to have clean sound and keep minimal phase shift if it's possible. They do not affect dynamics of the signal or colorize the original sound, they just perform correction in frequency domain. BT (Bilinear Transform) filters will have no distortion at high frequencies but will have distorted (relative to the similar analog filter) amplitude and frequency chart. MT (Matched Z Tranfrorm) filters can distort the signal at high frequencies because high frequencies can get reflected from Nyquist Frequency and that may cause aliasing effect. In fact, It's not audible in most cases.

There are some recommendations that could be given when applying equalization:

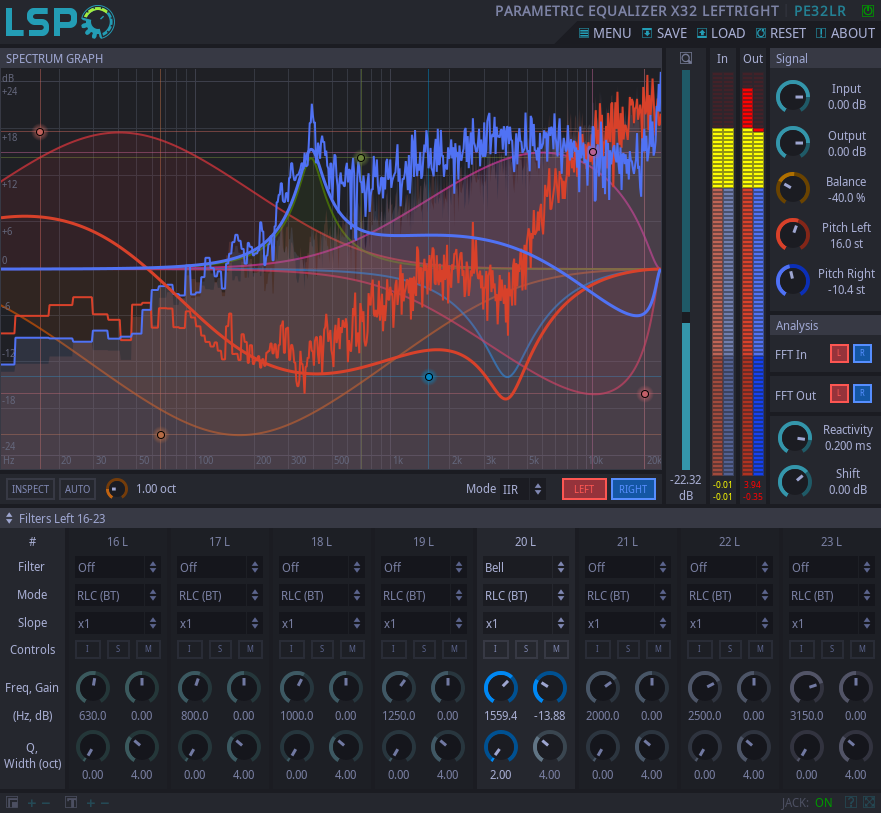
This plugin performs parametric equalization of stereo channel by applying individual equalization to left and right channels separately. Up to 32 filters are available for signal processing simultaneously.

Additional filter inspection feature with the controlled width of the bandpass filter allows to listen the frequency band around several filter types to make search and cut off resonances much easier:

It is also possible to switch filter between channels by selecting corresponding menu item in the popup menu ( ) above the filter's dot on the graph.

The steepness of the filter is depending on the type of the filter selected, it's slope and Q factor.

There is a simple rule that allows to compute the steepness of IIR (recursive) low-pass or high-pass filter which consists of so-called poles and zeros:

That allows to make the following conclusions:

There is a table that specifies characteristics of lowpass filters depending on the selected filter mode and slope.

Mode Poles Slope (dB/oct)
x1 x2 x3 x4 x1 x2 x3 x4
RLC 2 4 6 8 -12 -24 -36 -48
BWC 2 4 6 8 -12 -24 -36 -48
LRX 4 8 12 16 -24 -48 -72 -96
APO 2 2 2 2 -12 -12 -12 -12

Adjusting q can give additional steepness to the curve but making it too high gives extra non-linearity of the magnitude in the passed spectrum.

The frequency control feature allows to detect the note and the note detune the filter is operating with at the top of the graph area.

Additionally, mouse double-click on the graph area allows to add a filter with desired frequency and gain settings depending on the actual frequency value at the position of the mouse click:

Several filter parameters like type, mode, slope, inspection, solo and mute are also available for change from the context menu which can be displayed by the right mouse click over the filter's control dot in the graph area.

Meters:

Controls:

'Signal' section:

'Analysis' section:

'Filters' section: